I was thinking about LLM tokenization (as one does) and had a thought: We select the next output token for an LLM based on its likelihood, but (some) shorter tokens are more likely.
Why? Longer tokens can only complete one word, but some shorter tokens can complete many words. Those shorter common tokens1 are (correctly) learned to be higher-probability because they have the combined probability of any word they could complete. However, standard generation techniques will only consider a subset of probabilities (top-K) and scale the largest probabilities (temperature). Both of these will take the highest probabilities and increase them further, meaning short/common tokens become significantly more likely to be generated just because they're shorter.
I ran an experiment to investigate this, showing that the first-character distribution of words generated by nanoGPT2 is similar regardless of tokenization without top-K or temperature scaling, but if we use common settings (top-K=200 and temperature=0.8), we can increase the likelihood that a word starts with 'c' from 4% up to 10% just by tokenizing 'c' at the start of words separately from the rest of the word. I found similar but stronger effects when training on a tiny Shakespeare corpus.
This effect should also appear when a particular word is a common start to phrases. Techniques like beam search should help, but I don't think anyone does that in user-facing frontier models. I have a theory that this is part of the explanation for why AIs seem to all like the same words and have a similar style.
Why?
Feel free to skip to the experiment if this is all obvious.
Say you have a text corpus made up of conversations between Alice, Bob, Blake, Charles and Cathryn, and they're all equally likely to speak. There are 5 names, so in a model where you tokenize each name separately, the next-token probabilities for any name will be 20%.
If you tokenize the first letter separately (your vocab is ["A", "-lice", "B", "-ob", "-lake", "C", "-harles", "-athryn]), the probabilities will instead be:
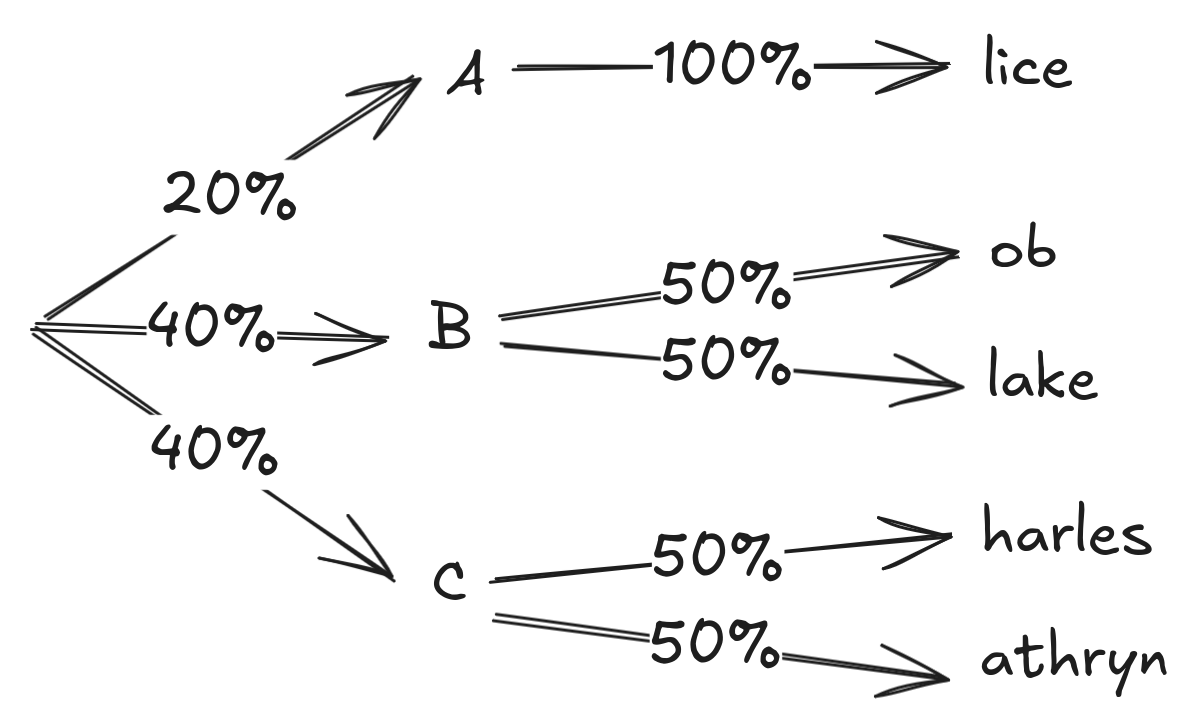
So far, so good, the full probability of each full name is the same (20%).
Top-K Sampling
Now, what if we only considered the top 23 tokens at each step?
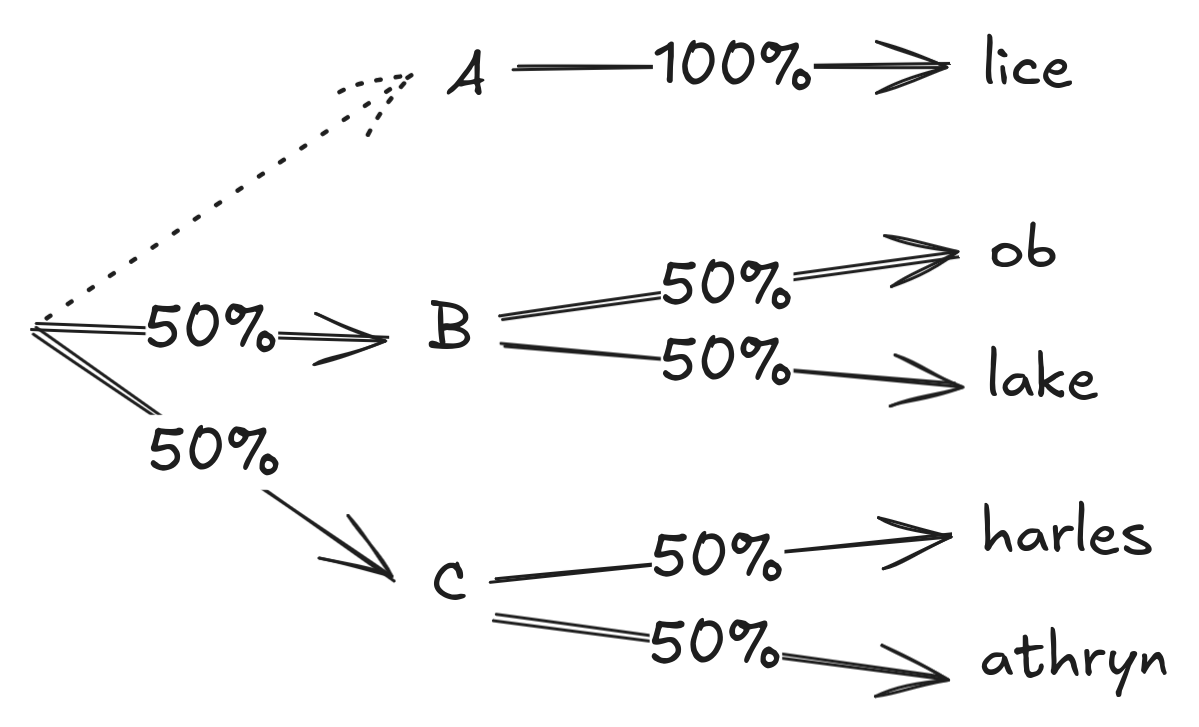
Now we've dropped the probability of predicting Alice from 20% to 0% and spread the probability between the other options.
Temperature < 1.0
tl;dr temperature makes more-common outputs even more common and less-common outputs even less common. Feel free to skip the details if you don't care.
We need to step back from probabilities for a second to explain temperature. An LLM actually outputs logits (numbers that can be negative or positive and don't necessarily add up to 1), which we then scale through softmax to get probabilities.
\[\text{softmax}(z_i) = \frac{e^{z_i}}{\sum_{j=1}^{n} e^{z_j}}\]
When using temperature scaling, the logits are first divided by the temperature (so numbers between 0 and 1 make the logit larger and numbers larger than 1 make it smaller). Since softmax exponentiates the logits, a small temperature scales larger logits more than smaller logits.
So, going back to our example, our logits might look like:
| Token | Logit | Probability |
|---|---|---|
| A | 0 | 20% |
| B | 0.693 | 40% |
| C | 0.693 | 40% |
But if we first scale them with temperature = 0.8, we get:
| Token | Logit | Scaled Logit | Probability |
|---|---|---|---|
| A | 0 | 0 | 17.4% |
| B | 0.693 | 0.866 | 41.3% |
| C | 0.693 | 0.866 | 41.3% |
Again, the LLM is biased to pick names not starting with A.
The Experiment
Theory is all well and good, but what if we actually try it? To prove this, I forked nanoGPT and set up two custom tokenizers:
- The control tokenizer lowercases everything, splits words on whitespace, tokenizes digits separately, and then trains a normal BPE tokenizer.
- The test tokenizer does the same, but forces words starting with a particular character to tokenize that initial character separately. I chose the letter "c", so words like "cat" would be forced to tokenize as [c, at].
I trained a model with GPT-2 architecture for 21,000 iterations4 on OpenWebText using each tokenizer.
Once each model was trained, I sampled 1000 separate 200 character outputs, then split the words and counted what proportion of words started with each letter. I repeated this with the following parameter combinations
| Temperature | Top-K |
|---|---|
| 1.0 | ∞ |
| 1.0 | 200 |
| 0.8 | 200 |
Note that temperature=1.0 and K=∞ corresponds to using the raw learned probabilities. 0.8 and 200 were chosen because they're fairly standard choices for these parameters.
Results
You can see the raw results for each model and set of sampling parameters here. Since we chose to tokenize "c" separately, I predicted that words starting with "c" should be more common in the test model than the control model, and this effect should increase as the temperature and top-K parameters drop.
Here's the top 10 initial characters in words and how their probability changes between the control and test model.
| Initial Character | Test Delta K=∞ T=1.0 | Test Delta K=200 T=1.0 | Test Delta K=200 T=0.8 |
|---|---|---|---|
| t | 1% | 1% | 1% |
| a | -1% | -1% | -1% |
| s | 0% | 0% | 0% |
| i | 0% | 0% | 0% |
| o | 0% | 0% | 0% |
| c | 0% | 3% | 6% |
| w | 0% | 0% | 0% |
| b | 0% | 0% | 0% |
| p | 0% | 0% | -1% |
| f | 0% | 0% | 0% |
See more detailed table here and raw data here.
So, this provides empirical validation that top-K with K=200 or temperature=0.8, breaking a token into smaller pieces makes it more likely to be chosen.
Shakespeare Experiment
The results above are more representative of a real model, but I was able to train small models on this Shakespeare dataset much faster, which let me run the same experiment above with more letters.
Each model trained until the validation loss started increasing, which was around 1,000 iterations.
Results
In this case, I only generated 100 samples of 100 tokens each, and all samples used K=200. Each row is the results for a test model using a tokenizer which forces the given letter to tokenize separately at the start of words.
| Letter | Control Frequency | Test T=1.0 | Test T=0.8 | Test T=0.1 |
|---|---|---|---|---|
| c | 2% | 5% | 8% | 43% |
| t | 15% | 18% | 28% | 53% |
| w | ~0% | 8% | 13% | 31% |
Looking through the output, the results are extremely obvious. Normal output has very few C-names, but if you force "c" to tokenize separately, suddenly you have a lot of conversations between clowns and Capulets. Similarly, initial-W tokenization suddenly has characters talking about the world a lot.
Why Does It Matter?
I suspect this has something to do with "LLM style". LLMs may be pushed to select "slop" words because those words have more possible endings, even if none of those endings are the best one.
It also seems concerning that such a small and seemingly-unimportant change to the tokenizer can have an unexpectedly large effect on outputs.
Also, as a BPE-tokenization-hater, I think it's interesting that this is a case where character-level transformers may be worse5, although models that try to group tokens so they're equally "surprising" might make this better.
Specifically, shorter tokens that the model is trained to use. There are a lot of short tokens that a model won't usually use because it was trained to use longer ones (for example, in a standard model, "c" is a short token, but it's not one that the model will use very often because it was trained to prefer tokens like "cat").I'm thinking of cases like splitting an "un-" or "non-" prefix into a separate token instead of having hundreds of individual tokens starting with "un-" and "non-", or cases where words are uncommon enough that the full word isn't a token. ↩
The same architecture as GPT-2 but trained on OpenWebText. ↩
Top-2 is unrealistic, but I don't want this example to get too long. See below where I show empirically that top-200 causes this effect in practice. ↩
I initially trained one model until the validation loss started increasing, which happened to be 21,000 iterations, then realized I should train the other model for the same number of iterations. ↩
I hope you like words starting with e. ↩